ML Advanced Probabilistic Methods

1. Bayesian Networks

• Bayesian network:
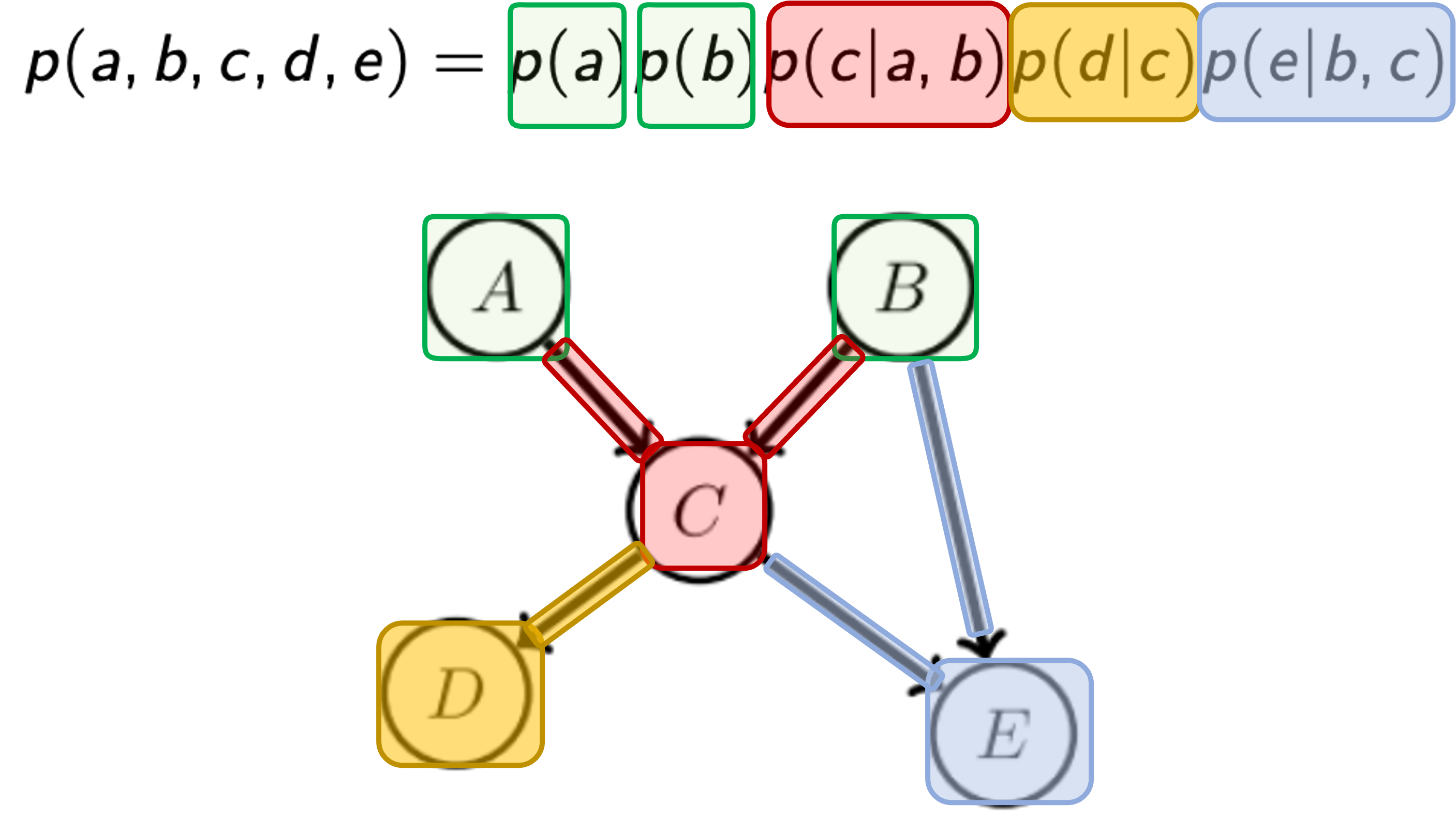
  It is a Directed Acyclic Graph (DAG) that describes the relationship between variables via their joint distribution. This distribution factorizes according to the graph in the way specified by the conditionals extracted from the parents of each node (random variable).
  • Why use BNs:
    1- Because of Computational Efficiency. In joint Distribution for growing number of random variables, the number of combination of combinations grows exponentially.(BNs, compact and concise way of representing joint distributions)
    2- Makes it easy to understand the model structure and dependencies conceptually. Efficient and optimized algorithms for graphs analysis.

• Independence A ⫫ B or A ⫫ B | E
  Some questions about independence and conditional independence that we could ask based on a Directed Acylic Graph (DAG):
  • A ⫫ B: Are A and B marginally independent?
  • A ⫫ B | E: Could we say A and B are independent when conditioned on E?
  • D ⫫ E | C: Are D and E independent given C?
  • A ⫫ B | C: Are A and B independent given C? If this statement holds then the joint distribution of a and b conditionally on c p(a,b|c) factorizes into product of p(a|c)p(b|c) for all possible values a ∈ A, b ∈ B, c ∈ C.
  Based on the above DAG, we can make the following statements about independence and conditional independence:
  • A ⫫ B: Yes, A and B are marginally independent.
  • A ⫫ B | E: No, A and B are not conditionally independent given E.
  • D ⫫ E | C: Yes, D and E and conditionally independent given C.
  • A ⫫ B | C: No, A and B are not conditionally independent given C.
  Examples:
  

  Example 1

  

  Example 2

  

Central concepts for determining conditional independence:

• D-connection and D-separation
• Note: For arbitrary variables X and Y to be conditionally independent given Z (hence d-separated), all paths between X and Y must be blocked given Z.

Markov Blanket:

• The markov blanket of a variable X contains its parents, children, and parents of its children.
• Conceptually, this blanket contains sufficient information for inference to be performed on the variable X. This is especially helpful when the total number of variables in the DAG is large.

Ways to select between models

Marginalization:
getting rid of one of the variables in joint probability distribution with summation over the other parameter

Independence:
p(b)p(m)=p(b, m)